面试题65. 不用加减乘除做加法(一般)

写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。

示例:

输入: a = 1, b = 1
输出: 2

提示：

a, b 均可能是负数或 0
结果不会溢出 32 位整数

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof

思路：

本题考察对位运算的灵活使用，即使用位运算实现加法。
设两数字的二进制形式 a,b ，其求和 s=a+b ，a(i) 代表 a 的二进制第 i位，则分为以下四种情况：

a(i) b(i) 无进位和 n(i) 进位c(i+1)
00 00 00 00
00 11 11 00
11 00 11 00
11 11 00 11

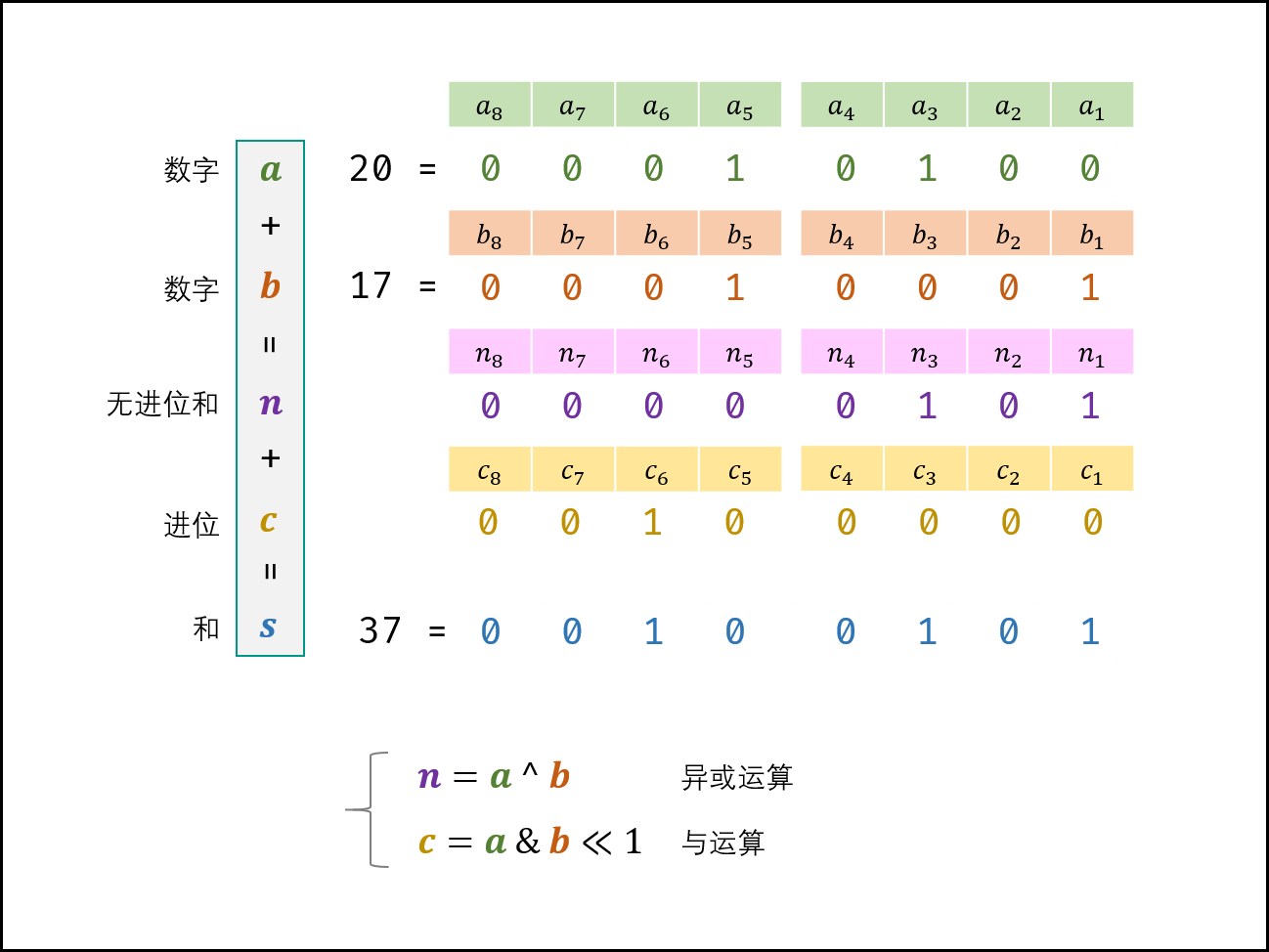
观察发现，无进位和 与 异或运算 规律相同，进位 和 与运算 规律相同（并需左移一位）。因此，无进位和 n 与进位 c 的计算公式如下；
$$
\begin{cases} n = a \oplus b & 非进位和：异或运算 \ c = a & b << 1 & 进位：与运算 + 左移一位 \end{cases}
$$
（和 s ）=（非进位和 n ）+（进位 c ）。即可将 s = a + b 转化为：

​ s=a+b⇒s=n+c

循环求 n 和 c，直至进位 c=0 ；此时 s = n ，返回 n 即可。

作者：jyd
链接：https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/solution/mian-shi-ti-65-bu-yong-jia-jian-cheng-chu-zuo-ji-7/

Q ： 若数字 a 和 b 中有负数，则变成了减法，如何处理？
A ： 在计算机系统中，数值一律用 补码 来表示和存储。补码的优势： 加法、减法可以统一处理（CPU只有加法器）。因此，以上方法 同时适用于正数和负数的加法 。

复杂度分析：
时间复杂度 O(N) ： 其中 N 为循环次数。
空间复杂度 O(1) ： 使用常数大小的额外空间。

回看记录200726

记得不是很清楚，进位那一个操作需要多记

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int add(int a, int b) {
        //明显考察位运算
        while(b!=0){//b当作进位接收，当没进位时结束
            //求和,不考虑进位
            int sum = (a^b);
            //计算进位，位与运算，在向左移一位，1，1时进位
            b = ((a&b)<<1);
            a = sum;
        }
        return a;
    }
}