面试题36. 二叉搜索树与双向链表/426(一般)

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

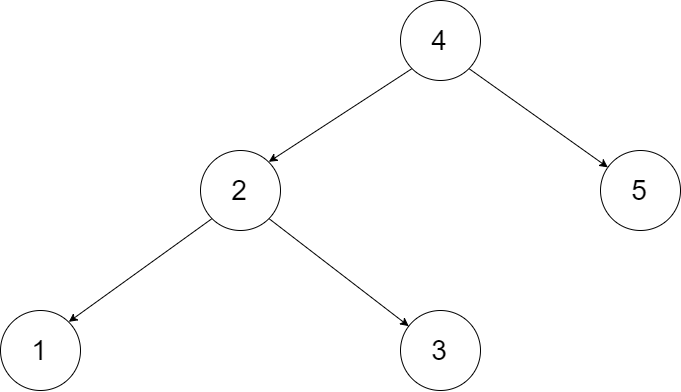
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

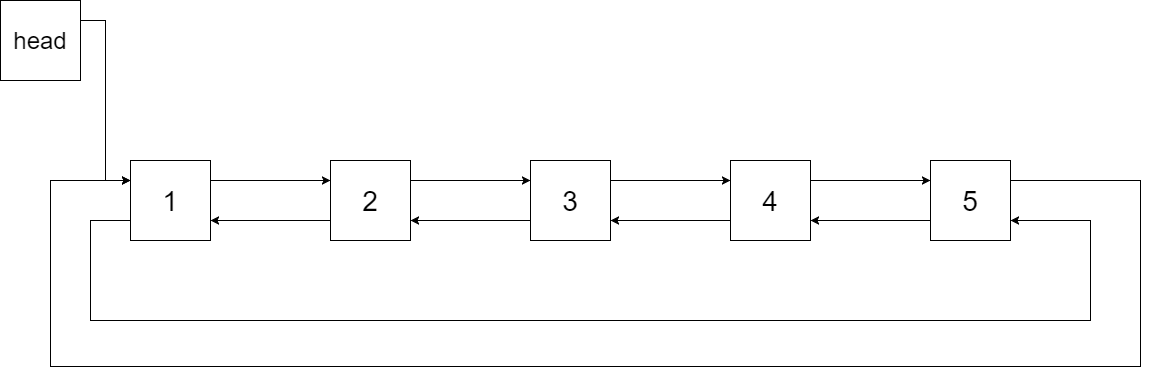
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

注意：本题与主站 426 题相同：https://leetcode-cn.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/

注意：此题对比原题有改动。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof

思路：

将 二叉搜索树 转换成一个 “排序的循环双向链表” ，其中包含三个要素：

排序链表： 节点应从小到大排序，因此应使用 中序遍历 “从小到大”访问树的节点；
双向链表： 在构建相邻节点（设前驱节点pre ，当前节点 cur ）关系时，不仅应 pre.right = cur ，也应 cur.left = pre
循环链表： 设链表头节点 head 和尾节点 tail ，则应构建 head.left = tail 和 tail.right=head

作者：jyd
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/solution/mian-shi-ti-36-er-cha-sou-suo-shu-yu-shuang-xian-5/

dfs(cur): 递归法中序遍历；

  1. 终止条件： 当节点 cur 为空，代表越过叶节点，直接返回；
  2. 递归左子树，即 dfs(cur.left) ；
  3. 构建链表：
    • 当 pre 为空时： 代表正在访问链表头节点，记为 head 。
    • 当 pre 不为空时： 修改双向节点引用，即 pre.right = cur， cur.left = pre；
    • 保存 cur ： 更新 pre=cur ，即节点 cur 是后继节点的 pre ；
  4. 递归右子树，即 dfs(cur.left) ；

treeToDoublyList(root)：

  1. 特例处理： 若节点root 为空，则直接返回；
  2. 初始化： 空节点pre ；
  3. 转化为双向链表： 调用 dfs(root) ；
  4. 构建循环链表： 中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可。
  5. 返回值： 返回链表的头节点 head 即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    Node pre=null,head = null;//pre变量来记录遍历过程的上一个节点
    public Node treeToDoublyList(Node root) {
        if(root==null)
            return null;
        dfs(root);//dfs
        pre.right = head;
        head.left = pre;
        return head; 
    }

    void dfs(Node root){
        if(root==null)
            return ;
        dfs(root.left);
        if(pre!=null)
            pre.right = root;//pre指向当前，然后当前指向pre
        else
            head = root;//找到头节点
        root.left=pre;
        pre = root;//将pre指针指向当前节点
        dfs(root.right);
    }
}