343. 整数拆分/面试题14- I. 剪绳子/面试题14- II. 剪绳子 II(一般)

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

说明：剪绳子2，要考虑大数情况

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1:

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/integer-break

思路1：

带记忆化的递推（未写）

思路2：

动态规划思路，也就是思路1的逆过程，将记忆化的从上到下，变为从下到上

建立一维动态数组 dp：

边界条件：dp[1] = dp[2] = 1，表示长度为 2 的绳子最大乘积为 1；
状态转移方程：dp[i] = max(dp[i], max((i - j) * j, j * dp[i - j]))，可以这样理解：

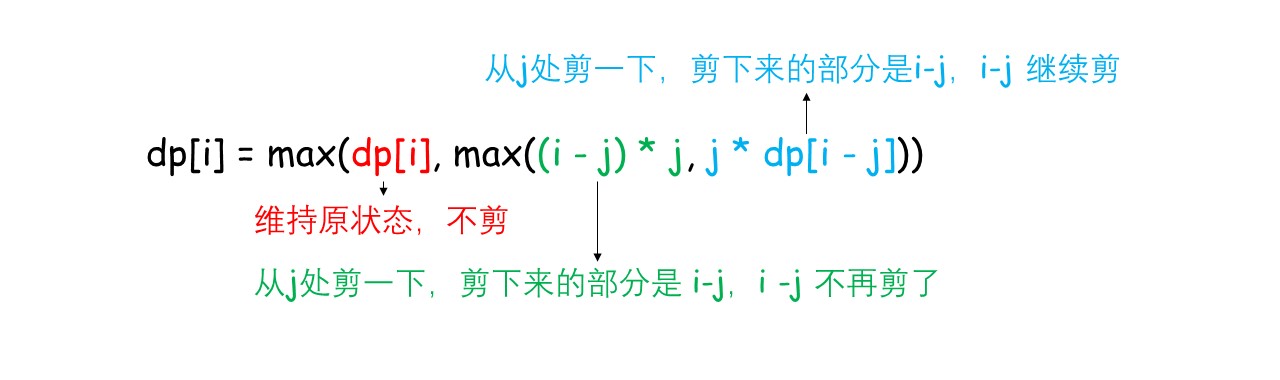
思路3：

贪心，（未写）

思路4：

大数的，用贪心最好，dp难写（未写）

代码1：

1

代码2：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int cuttingRope(int n) {
        int[] dp = new int[n+1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for ( int j = 1; j <= i - 1; j++) {
                dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));
            }
        }
        return dp[n];
    }
}

代码3：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//大数情况，dp方法，但还是推荐用贪心算法
import java.math.BigInteger;
class Solution {
    public int cuttingRope(int n) {
        BigInteger dp[] = new BigInteger[n+1];
        Arrays.fill(dp, BigInteger.valueOf(1));
        for (int i = 3; i <= n; i++) {
            for ( int j = 1; j <= i - 1; j++) {
                // dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));
                dp[i] = dp[i].max(BigInteger.valueOf(j * (i - j))).max(dp[i - j].multiply(BigInteger.valueOf(j)));
            }
        }
        return  dp[n].mod(BigInteger.valueOf(1000000007)).intValue();
    }
}