65. 有效数字/面试题20. 表示数值的字符串(困难)

验证给定的字符串是否可以解释为十进制数字。

例如:

"0" => true
" 0.1 " => true
"abc" => false
"1 a" => false
"2e10" => true
" -90e3 " => true
" 1e" => false
"e3" => false
" 6e-1" => true
" 99e2.5 " => false
"53.5e93" => true
" --6 " => false
"-+3" => false
"95a54e53" => false

说明: 我们有意将问题陈述地比较模糊。在实现代码之前，你应当事先思考所有可能的情况。这里给出一份可能存在于有效十进制数字中的字符列表：

数字 0-9
指数 - "e"
正/负号 - "+"/"-"
小数点 - "."
当然，在输入中，这些字符的上下文也很重要。

更新于 2015-02-10:
C++函数的形式已经更新了。如果你仍然看见你的函

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/valid-number

思路：

解题思路：
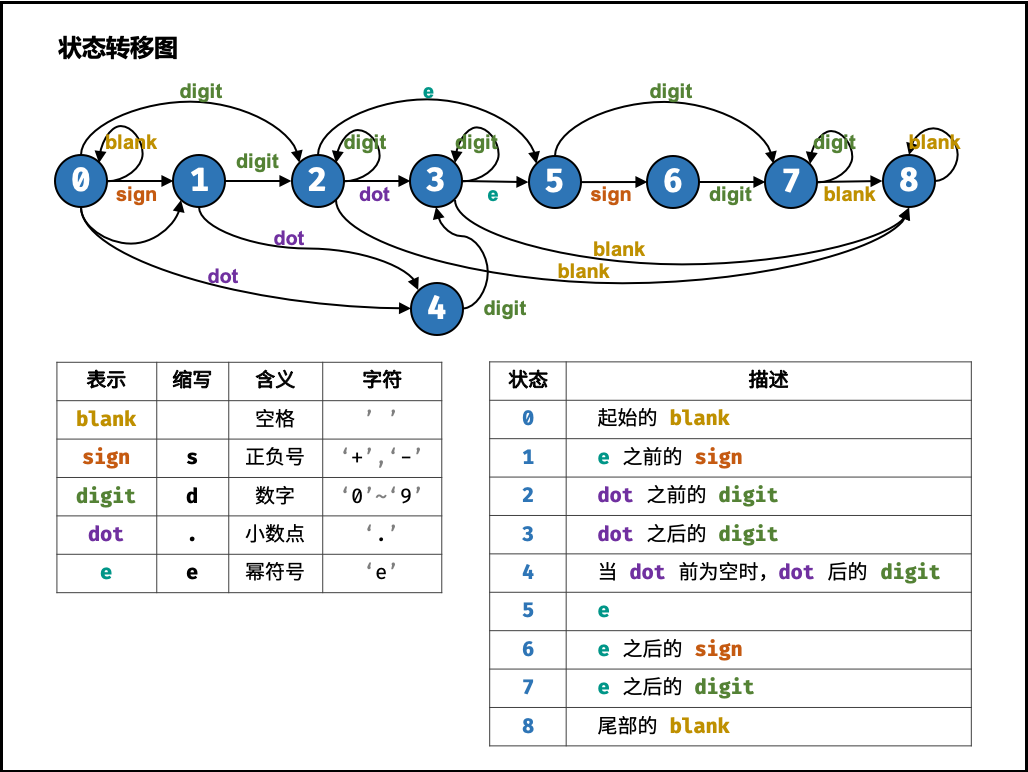
本题使用有限状态自动机。根据字符类型和合法数值的特点，先定义状态，再画出状态转移图，最后编写代码即可。

字符类型：

空格 「 」、数字「 0—9 」 、正负号 「 +− 」 、小数点 「 . 」 、幂符号 「 e 」 。

状态定义：

按照字符串从左到右的顺序，定义以下 9 种状态。

  1. 开始的空格
  2. 幂符号前的正负号
  3. 小数点前的数字
  4. 小数点、小数点后的数字
  5. 当小数点前为空格时，小数点、小数点后的数字
  6. 幂符号
  7. 幂符号后的正负号
  8. 幂符号后的数字
  9. 结尾的空格

结束状态：

合法的结束状态有 2, 3, 7, 8 。

算法流程：

  1. 初始化：
    1. 状态转移表 states ： 设 states[i] ，其中 i 为所处状态， states[i] 使用哈希表存储可转移至的状态。键值对 (key,value) 含义：若输入key ，则可从状态 i 转移至状态 value。
    2. 当前状态 p ： 起始状态初始化为 p=0 。
  2. 状态转移循环： 遍历字符串 s 的每个字符 c 。
    1. 记录字符类型 t ： 分为三种情况。
      • 当 c 为正负号时，t = ‘s’ ;
      • 当 c 为数字时，t = ‘d’ ;
      • 否则，t = c ，即用字符本身表示字符类型 ;
    2. 终止条件： 若字符类型 t 不在哈希表 states[p] 中，说明无法转移至下一状态，因此直接返回 False 。
    3. 状态转移： 状态 p 转移至 states[p] [t] 。
  3. 返回值： 跳出循环后，若状态p∈2,3,7,8 ，说明结尾合法，返回 True ，否则返回 False 。

复杂度分析：
时间复杂度 O(N) ： 其中 N 为字符串 s 的长度，判断需遍历字符串，每轮状态转移的使用 O(1) 时间。
空间复杂度 O(1) ： states 和 p 使用常数大小的额外空间。

作者：jyd
链接：https://leetcode-cn.com/problems/biao-shi-shu-zhi-de-zi-fu-chuan-lcof/solution/mian-shi-ti-20-biao-shi-shu-zhi-de-zi-fu-chuan-y-2/

本代码和思路全部参考题解，请注意掌握状态机这一解题方法

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean isNumber(String s) {
        Map[] states = {
            new HashMap<>() {{ put(' ', 0); put('s', 1); put('d', 2); put('.', 4); }}, // 0.
            new HashMap<>() {{ put('d', 2); put('.', 4); }},                           // 1.
            new HashMap<>() {{ put('d', 2); put('.', 3); put('e', 5); put(' ', 8); }}, // 2.
            new HashMap<>() {{ put('d', 3); put('e', 5); put(' ', 8); }},              // 3.
            new HashMap<>() {{ put('d', 3); }},                                        // 4.
            new HashMap<>() {{ put('s', 6); put('d', 7); }},                           // 5.
            new HashMap<>() {{ put('d', 7); }},                                        // 6.
            new HashMap<>() {{ put('d', 7); put(' ', 8); }},                           // 7.
            new HashMap<>() {{ put(' ', 8); }}                                         // 8.
        };
        int p = 0;
        char t;
        for(char c : s.toCharArray()) {
            if(c >= '0' && c <= '9') t = 'd';
            else if(c == '+' || c == '-') t = 's';
            else t = c;
            if(!states[p].containsKey(t)) return false;
            p = (int)states[p].get(t);
        }
        return p == 2 || p == 3 || p == 7 || p == 8;
    }
}