233. 数字 1 的个数/剑指 Offer 43. 1～n整数中1出现的次数(困难)

输入一个非负整数 n ，求1～n这n个整数的十进制表示中1出现的次数。

例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

示例 1：

输入：n = 12
输出：5

示例 2：

输入：n = 13
输出：6

限制：

1 <= n < 2^31

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof

思路：

某位中 11 出现次数的计算方法：

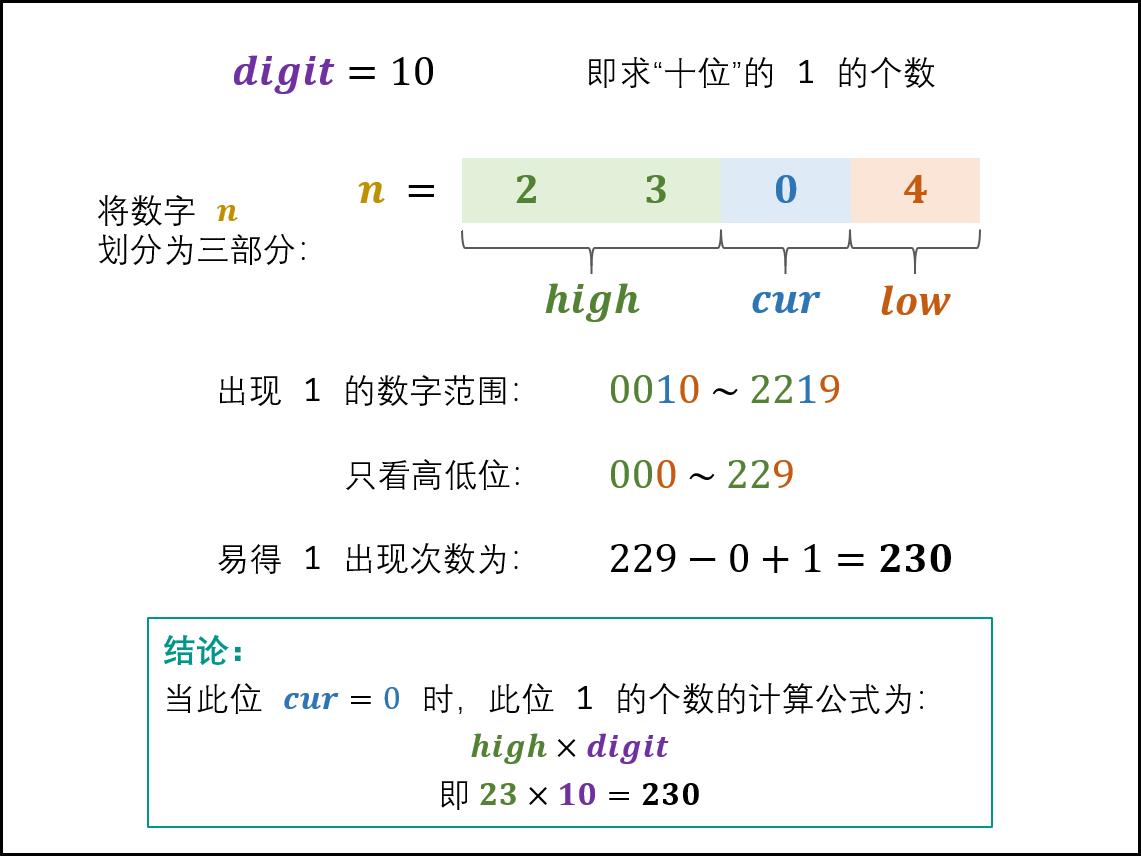
当 cur = 0 时： 此位 1 的出现次数只由高位 high 决定，计算公式为：high×digit

如下图所示，以 n = 2304为例，求 digit = 10（即十位）的 11 出现次数。

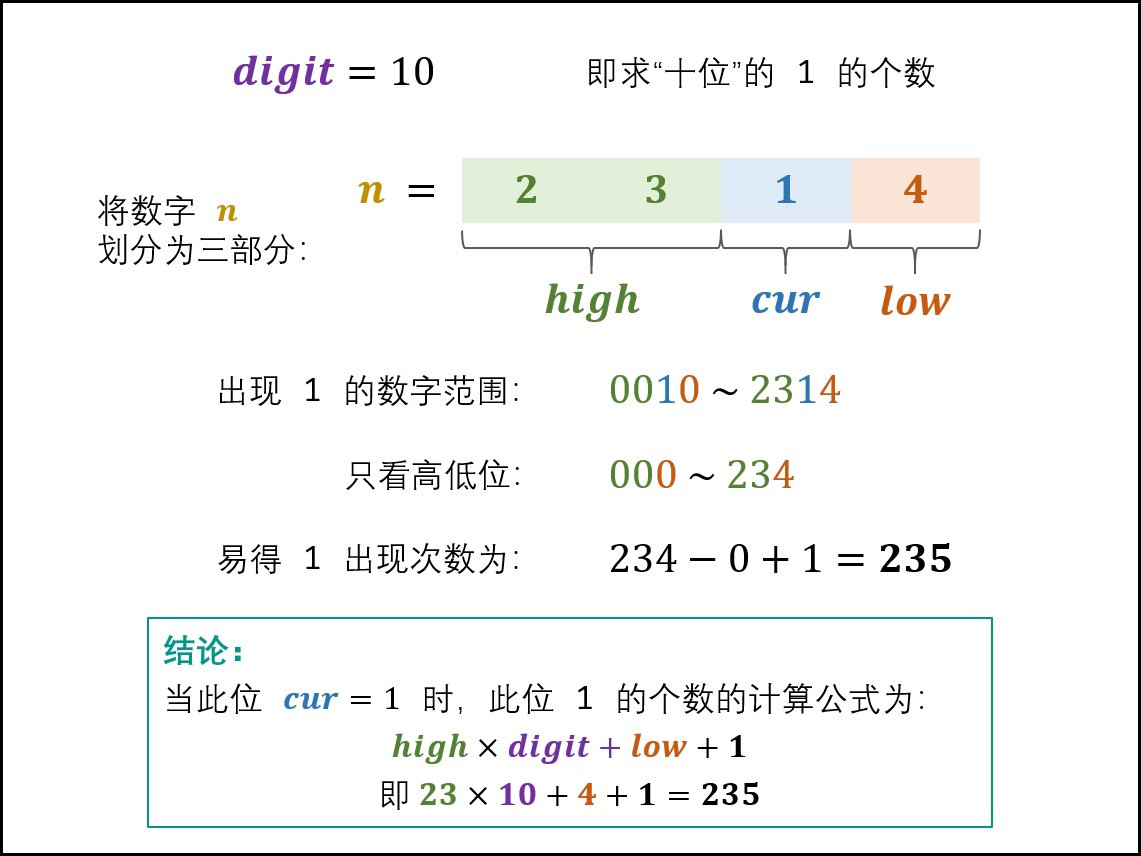
当 cur = 1时： 此位 1 的出现次数由高位 high 和低位 low 决定，计算公式为：
high×digit+low+1

如下图所示，以n=2314 为例，求 digit=10 （即十位）的 1 出现次数。

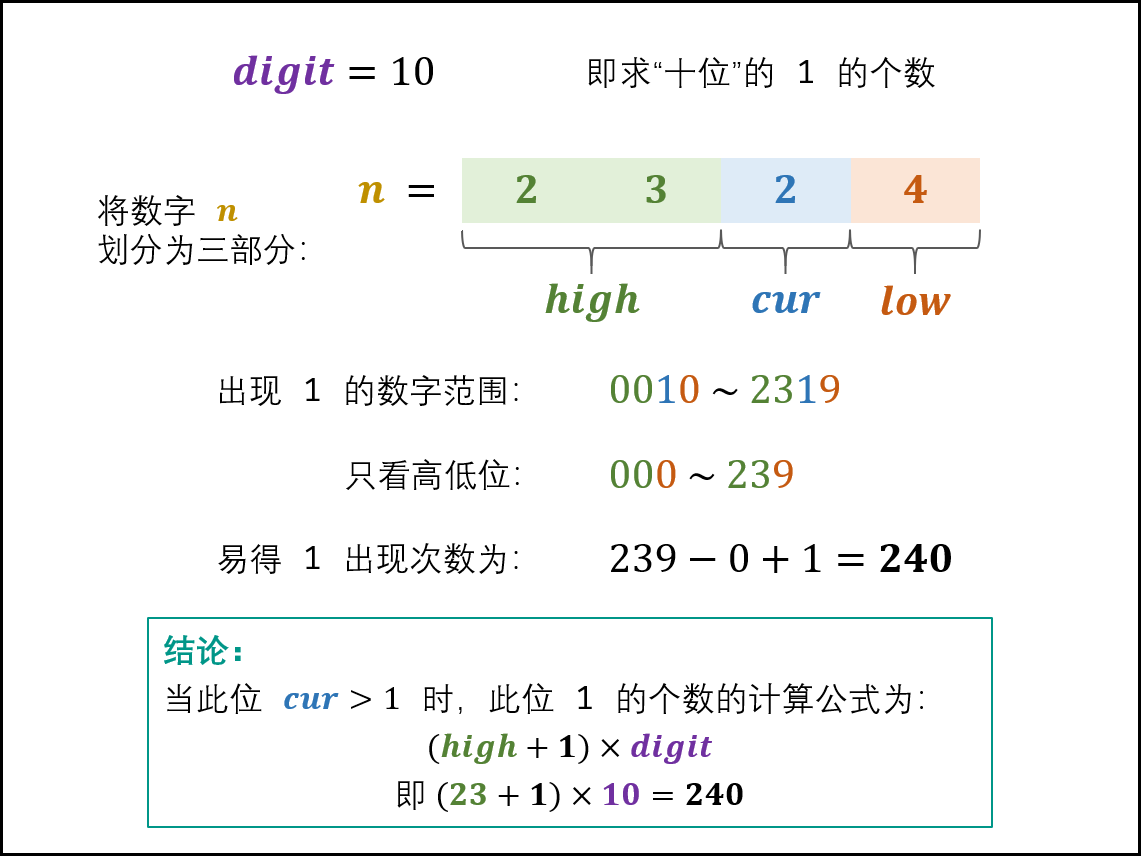
当 cur=2,3,⋯,9 时： 此位 1 的出现次数只由高位 high 决定，计算公式为：
(high+1)×digit

如下图所示，以 n=2324 为例，求 digit=10 （即十位）的 11 出现次数。

变量递推公式：
设计按照 “个位、十位、…” 的顺序计算，则 high / cur / low / digit 应初始化为：

1
2
3
4
high = n // 10
cur = n % 10
low = 0
digit = 1 # 个位

因此，从个位到最高位的变量递推公式为：

1
2
3
4
5
while high != 0 or cur != 0: # 当 high 和 cur 同时为 0 时，说明已经越过最高位，因此跳出
   low += cur * digit # 将 cur 加入 low ，组成下轮 low
   cur = high % 10 # 下轮 cur 是本轮 high 的最低位
   high //= 10 # 将本轮 high 最低位删除，得到下轮 high
   digit *= 10 # 位因子每轮 × 10

作者：jyd
链接：https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/solution/mian-shi-ti-43-1n-zheng-shu-zhong-1-chu-xian-de-2/

注意

这题真的头疼，数学推理出来

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    //真的头疼
    public int countDigitOne(int n) {
        if(n<=0)
            return 0;
        int high = n/10,cur=n%10,low=0;//分为三段
        int res =0,digit=1;
        while(high!=0 || cur!=0){
            if(cur==0)
                res +=high*digit;
            else if(cur==1)
                res +=high*digit+low+1;
            else
                res +=(high+1)*digit;
            low +=cur*digit;
            cur = high%10;
            high/=10;
            digit*=10;
        }
        return res;
    }
}